How to Interpret a Logistic Regression Model Coefficient
To interpret a logistic regression coefficient you only need three key things to understand. 1. Logistic function, 2. Logit function, and 3. Odds. If you understand these three concepts then you should be able to interpret any logistic regression model! In this article I’ll cover all these concepts and show how to interpret a coefficient of a logistic regression model. Although the formulae and equations may look daunting at a first glance the reason I have some extra lines of equations is that I have shown all the intermediate steps before writing the final form of an equation to make them easy to understand. Ok, enough talking, now let’s dive into the beautiful world of logistic regression:-) I’ll start with the standard logistic function.
Standard logistic function:
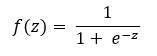
If we plot this function we get a curve like the following:

This s-shaped function is also called logistic sigmoid function. At first let’s see how we will use a logistic function to represent our regression equation.
Let’s assume our linear regression equation is in this form:
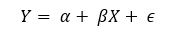
Here, Y: dependent variable, X: independent variable, β: coefficient, and ∈: error term.
Now, by using the standard logistic function we can transform our regression problem into the following:

As we see in the equation above, in case of logistic regression, instead of using Y directly on the left side of our equation we use f(Y) which is probability of Y. Specifically, probability of Y being in the positive class or p(Y=1). Simply we can write it as p to avoid some verbiage. Hence, we can write the logistic regression equation in the following way:
Logistic Regression (LR) Equation:
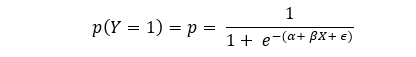
Now let’s rewrite the above in the following way:
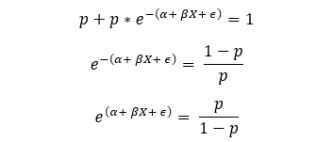
Taking natural log on both sides:
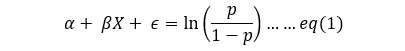
This equation ,eq(1), is another form of logistic regression equation where left-hand side is same as in our linear regression equation. Now, the right-hand-side of this equation has a special term called the logit. Logit is a function such as:
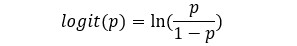
Logit function is defined as the natural logarithm (log with base e or ln) of odds. Odds is a ratio of probabilities of something happening and not happening. To be specific, odds would be a ratio of probabilities of Y being 1 and 0. As probabilities of an event sum up to 1, we can say that if we sum up probability of positive and negative classes for a given binary dependent variable we will get 1. Utilizing these facts we can write:
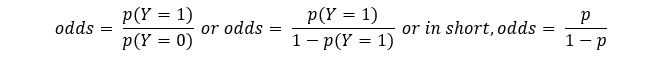
In summary, the main takeaway in this section is that in case of logistic regression, our dependent variable is logit or log of odds.
How to interpret coefficients:
We will start with interpretation of a linear regression model coefficient and later move on to interpretation of logistic regression coefficients.
Interpretation of linear regression coefficients:
Let’s assume our problem for linear regression model is that we are trying to predict how much money a family spends on purchasing a house. So, our dependent variable is money (in USD) spent on house purchase. For the sake of simplicity, let’s also assume we have a single binary independent variable which takes value of 1 if a family has kid(s) or takes value of 0 if a family does not.
A sample linear regression equation for our problem could be like this:
Spending on house purchase in USD = 20,000 + 50,000*kids
Here, kids is the independent variable which takes value of 1 if a family has kids (X=1) and value of 0 if a family does not (X=0). Coefficient of kids variable is +50,000. Thus, we can interpret the above example in this way: Given everything else held constant, our model predicts a family with kids spends $50,000 more on house purchase than a family with no kids.
From above example we can see that for our problem the coefficient gives the difference between the spending on a house purchase for a family with kids vs a family with no kids. Using the example, we can write a generic equation for coefficient β:
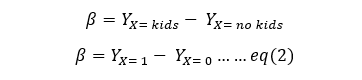
This equation will be handy when we interpret coefficients of logistic regression. Next, we will discuss interpretation of logistic regression equation:
Coefficient in logistic regression:
For logistic regression model our dependent variable is binary or categorical for classification tasks in machine learning applications. Although it is possible to have continuous dependent variables in logistic regression models, it is outside of the scope of this article.
We can modify our problem statement slightly by taking a binary dependent variable. Our problem statement for logistic regression model is that we are trying to predict whether a given family purchases a house or not. Our dependent variable is binary which takes value of 1 for a family who purchases a house and value of 0 for a family who does not purchase. Our independent variable, kids, remains the same.
Now I am rewriting the logistic regression equation derived in eq(1):
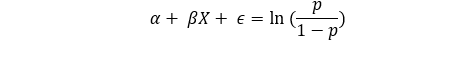
Here, the variable X is causing β amount of effect on the dependent variable logit(p) i.e. log(odds). So, a family with kids will have β amount of effect on log(odds) of purchasing a house. If the coefficient is positive then a family with kids will have higher log odds compared to a family without kids.
Similar to our linear regression example eq(2), we can write β in the following way:
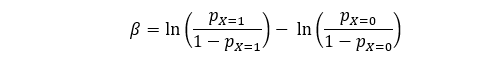
Using quotient rule of logarithm:
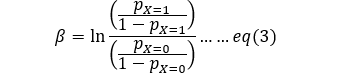
Here, if we recall the definition of odds, we actually have a ratio of odds in the above equation. For our kids variable, if we write the above equation in English it would look like this:
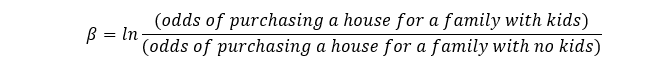
For easier interpretation we can do the following steps from eq(3):
Taking exponents on both sides:
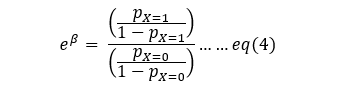
and finally,
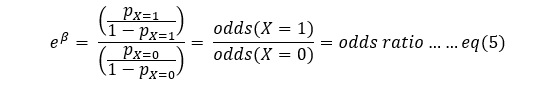
This is how the famous ‘odds ratio’ term comes into the picture of logistic regression! To interpret a coefficient of a logistic regression we need to find exponential of the coefficient and that exponential would give us odds ratio for a given independent variable.
Interpretation of a Logistic Regression coefficient for our example:
Before we proceed, please remember that for logistic regression our dependent variable is logit or log(odds). Similar to linear regression, we are again ignoring the error term, ϵ as we are dealing with predicted value of the dependent variable in the example.
Example Logistic Regression model equation:
Logit(y) = log(odds) = 0.4 + 0.8x
Here, the coefficient of x is 0.8. It means each unit increase in x increases log(odds) by 0.8. Now, utilizing eq(5), if we take the exponential of beta then we will get the odds ratio.
Now, exp(0.8) = 2.23
So, here, 2.23 is the odds ratio.
or 2.23 = odds of purchasing a house with kids/ odds of purchasing a house without kids
we can interpret 2.23 in the following way: keeping everything else constant, odds of purchasing a house is 2.23 times for a family with kids than the odds of purchasing a house for a family without kids. Or, we can say a family with kids is 2.23 times more likely to purchase a house than a family without kids. In other words, a family with kids is (2.23-1)/1 or 123% more likely to buy a house compared to a family without kids.
Now, you know how to interpret a logistic regression coefficient! But, what if our coefficient is negative? In the above example we have interpreted odds ratio when the coefficient is positive. Let’s take an example where a coefficient is negative:
Logit(y) = log(odds) = 0.5 – 0.2x
Assume that here our independent variable is job travel requirements of an individual where job travel requirements takes a value of 1 if an individual’s job requires frequent travels and value of 0 if it does not. Dependent variable is still very similar: takes a value of 1 if an individual owns a house and 0 if an individual does not.
Here exp(-0.2) = 0.135. If we interpret similarly, odds of purchasing a house is 0.135 times for an individual with a job that requires frequent travels than the odds of purchasing a house for an individual with a job that does not require frequent travels. Here, “0.135 times” is little hard to comprehend. In percentage we can say, individuals with jobs that require travels are (0.135-1)/1% or 86.5% less likely to buy a house than individuals with jobs that does not require frequent travels. Or, we can take inverse of exp(β) in the eq(5) to interpret in a more convenient way:
1/(exp(-0.2)) = 1/0.135 = 7.4
Now, we can say that individuals with no frequent travel requirements in jobs are 7.4 times more likely to buy a house than individuals with frequent travel requirements in jobs. We can find the percentage difference in the similar way. Individuals with no frequent travel requirements in jobs are 640% more likely to buy a house than individuals with frequent travel requirements in jobs.
Now, you know how to interpret a logistic regression coefficient! Here, I only covered independent variables that are binary, but, this same logic can be generalized to any other variable types including numerical and categorical. This article should help you to interpret any logistic regression model coefficients.